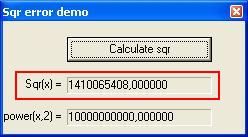
Normally one would expect the sqr function to throw an exception in case of an overflow. As a matter of fact, if you try to evaluate X*X where X=100000, you get an "integer overflow" complaint from the compiler because X*X=1e10 which is larger than (2^31)-1. However, if you use sqr(X) instead, the compiler happily calculates the result as... 1410065408! The sqr function does not catch integer overflows, instead, it provides the result that fits in 32 slots. Id est, it discards the remaining bits.
Let me explain: 1e10 is 1001010100000010111110010000000000 in binary. This is a number that requires 34 bits. However, integer has only 32 bits. So you kiss goodbye to the 33rd and 34th bits which leaves you with 01010100000010111110010000000000 which is... voila... 1410065408, exactly the result that sqr(X) gave us.
I advise to use the power function to be safe because power(X,2) gives the correct results.
Moral of the story: Always use functions like sqr, sqrt, cos, atan with extreme caution. Be sure to have explicit tests that just verify those functions, especially off limits.
You can download the executable and the source code of my little Delphi program if you don't believe me ;)


4 comments:
Denedim, gordum... Program sadece tek bir sayinin karesini hesaplayarak tarihe gecmeyi coktan haketmis :P
Ciddiyete donersek, programlar ne kadar buyuk ve karmasiklasirsa o kadar guvenilmez oluyorlar. Ben de SPSS'de hesaplanan istatistigin belirli bir durumda yanlis rapor edildigini kesfetmistim.
Her gecen gun bu tur programlar toplumsal ve bireysel hayatin daha da genis bir alaninda belirleyici oluyor. Lakin bu tur programlari gelistiren sirketlerin programi satmak disinda bir sorumluluklari var mi acaba diye merak ediyorum. Yarin obur gun SPSS ya da Delphi birseyleri yanlis yapti diye bir nukleer santral infilak ettiginde veya hic ise yaramayan bir ilac kullanilip bos yere tedavi beklendiginde bunun sorumlusu kim olacak. Programi dikkatsiz kullananlar mi yoksa ozensiz gelistiren gelistirenler mi?
Nükleer santral gibi insan hayatına mal olabilecek yerlerde kullanılan yazılımlar safety critical diye sınıflandırılırlar ve çok ciddi denetimlere taabi olurlar, buna compiler sertifikasyonu da dahil. Bu nedenle durum o kadar vahim değil.
Abisi,
bu yuzdendir ki, "multiprecision arithmetic" diye bir kavram ve bu kavramda hesap yapmani saglayan kutuphaneler mevcut. Ornegin (GMP~ Gnu Multiprecision Arithmetic, &c....) Antiparantez, ayrica "exact arithmetic", "variable precision arithmetic", ... gibi konularda ugrasan adamlar var.
Tahmin edersinki, herseyin bir bedeli oldugundan, bu kutuphanelerin goturusu calisma zamaninda uzama olmaktadir cunki hesaplar hardware'de degil bilakis bizzat software'de emule edilmektedir.
Bir de Python'a son versiyonda eklenen Decimal data tipini incelemende fayda var (http://www.python.org/dev/peps/pep-0327/)
Decimal data tipi hakkinda asil detayli bilgi (http://www2.hursley.ibm.com/decimal/) adresinde bulabilirsin.
respects
Sayıların bilgisayarda ifade ediliş biçiminden kaynaklanan problemlerden uzun zamandır haberdardım ancak sqr, sqrt, sin, cos gibi temel fonksiyonları sorgulamıyordum. Örneğin sqrt fonksiyonu x^2-n=0 denkleminin kökleri bulunarak çözülebiliyor (http://mathworld.wolfram.com/SquareRootAlgorithms.html)
Algoritmaların hangi durumlarda iyi sonuç verdiğini, ne zaman saçmalayabileceklerini tahmin etmek gerekiyor ki bunu yapmak sayıların precisionundan kaynaklanacak problemleri tahmin etmekten daha zor olabiliyor. Özellikle de temel fonksiyonları sorgulama gibi bir alışkanlığımız yoksa...
Post a Comment